513. 找树左下角的值

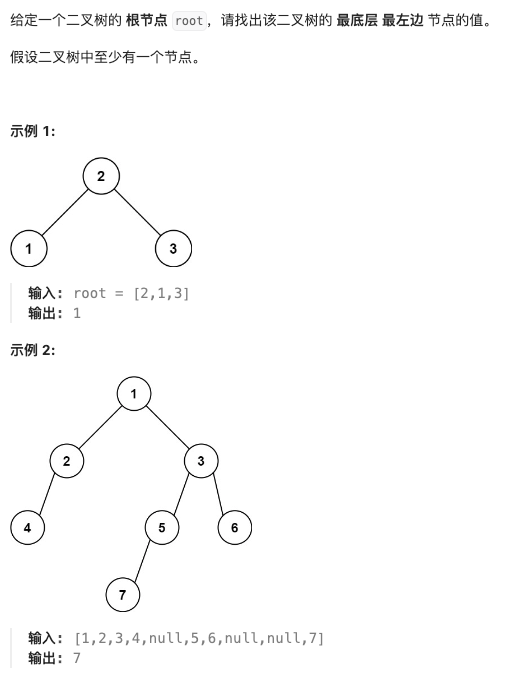思路：层序遍历最简单

class Solution:
    def findBottomLeftValue(self, root: Optional[TreeNode]) -> int:
        import collections 
        q = collections.deque([root])
        if not root:
            return 0
        
        while q:
            for i in range(len(q)):
                cur = q.popleft()
                if i == 0:
                    ret = cur.val
                if cur.left:
                    q.append(cur.left)
                if cur.right:
                    q.append(cur.right)
        return ret

递归法:

class Solution:
    def findBottomLeftValue(self, root: TreeNode) -> int:
        self.max_depth = float('-inf')
        self.result = None
        self.traversal(root, 0)
        return self.result
    
    def traversal(self, node, depth):
        if not node.left and not node.right:
            if depth > self.max_depth:
                self.max_depth = depth
                self.result = node.val
            return
        
        if node.left:
            self.traversal(node.left, depth+1)
        if node.right:
            self.traversal(node.right, depth+1)

112. 路径总和

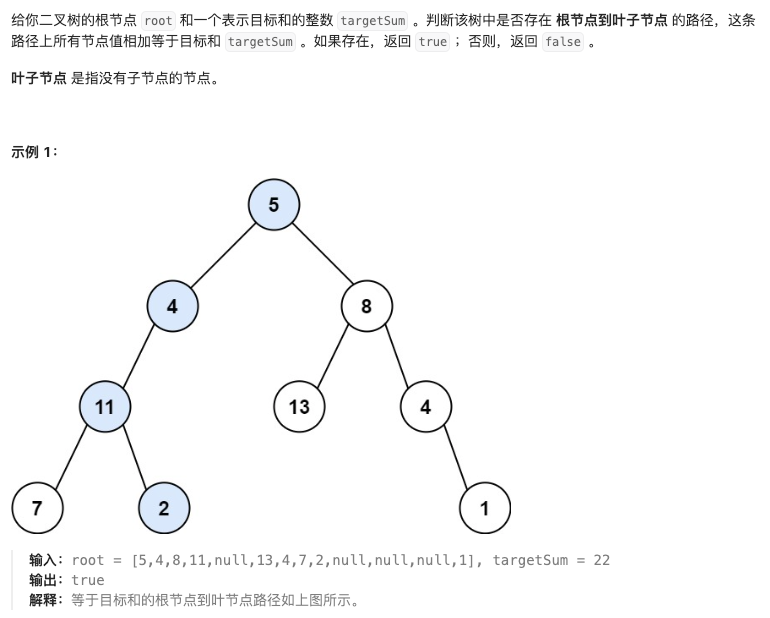思路：相当于求路径那一题，去计算路径的和

class Solution:
    def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
        result = False
        path = []
        if not root:
            return result
        result = self.traversal(root, path, result,targetSum)
        return result
        

    def traversal(self, cur, path, result,targetSum):
        path.append(cur.val)  # 中
        if not cur.left and not cur.right:  # 到达叶子节点
            sPath_sum = sum(path)
            if sPath_sum==targetSum:
                return True
        lret,rret=False,False   
        if cur.left:  # 左
            lret = self.traversal(cur.left, path, result,targetSum)
            path.pop()  # 回溯
        if cur.right:  # 右
            rret = self.traversal(cur.right, path, result, targetSum)
            path.pop()  # 回溯
        return True if lret or rret else False

106. 从中序与后序遍历序列构造二叉树

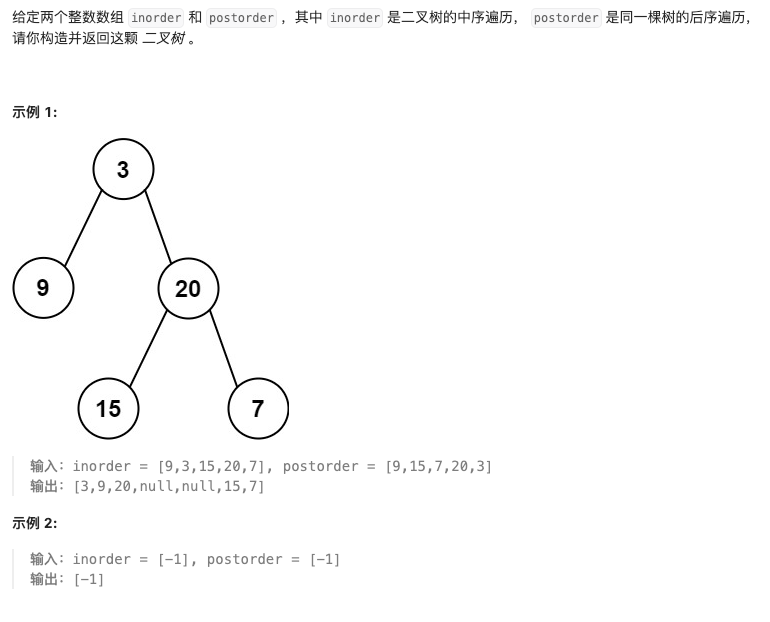思路：（用中序遍历去找根节点的index用来切割）

1. 分析后序遍历：后序遍历的最后一个元素是树的根节点。我们可以根据这个根节点将中序遍历序列分为左右两部分，左部分是根节点的左子树的中序遍历结果，右部分是根节点的右子树的中序遍历结果。

2. 分割中序遍历序列：根据上一步得到的根节点，我们可以将中序遍历序列分割为左子树的中序遍历和右子树的中序遍历。

3. 分割后序遍历序列：由于我们已经知道了左子树和右子树的中序遍历序列的长度，我们可以根据这个长度来分割后序遍历序列，得到左子树的后序遍历和右子树的后序遍历。

4. 递归构造子树：对左子树和右子树分别递归地执行上述步骤，直到所有的节点都被构造出来。

5. 返回根节点：当递归到最底层时，返回当前构造出的节点，这样一层一层地返回，最终得到完整的二叉树。

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
        if not inorder or not postorder:
            return None
        # 后序遍历的最后一个元素是根节点
        root_val = postorder[-1]
        root = TreeNode(root_val)
        # 在中序遍历中找到根节点的位置，这样可以分割左右子树
        index = inorder.index(root_val)
        # 递归构造左子树和右子树
        root.left = self.buildTree(inorder[:index], postorder[:index])
        root.right = self.buildTree(inorder[index+1:], postorder[index:-1])
        return root