235. 二叉搜索树的最近公共祖先

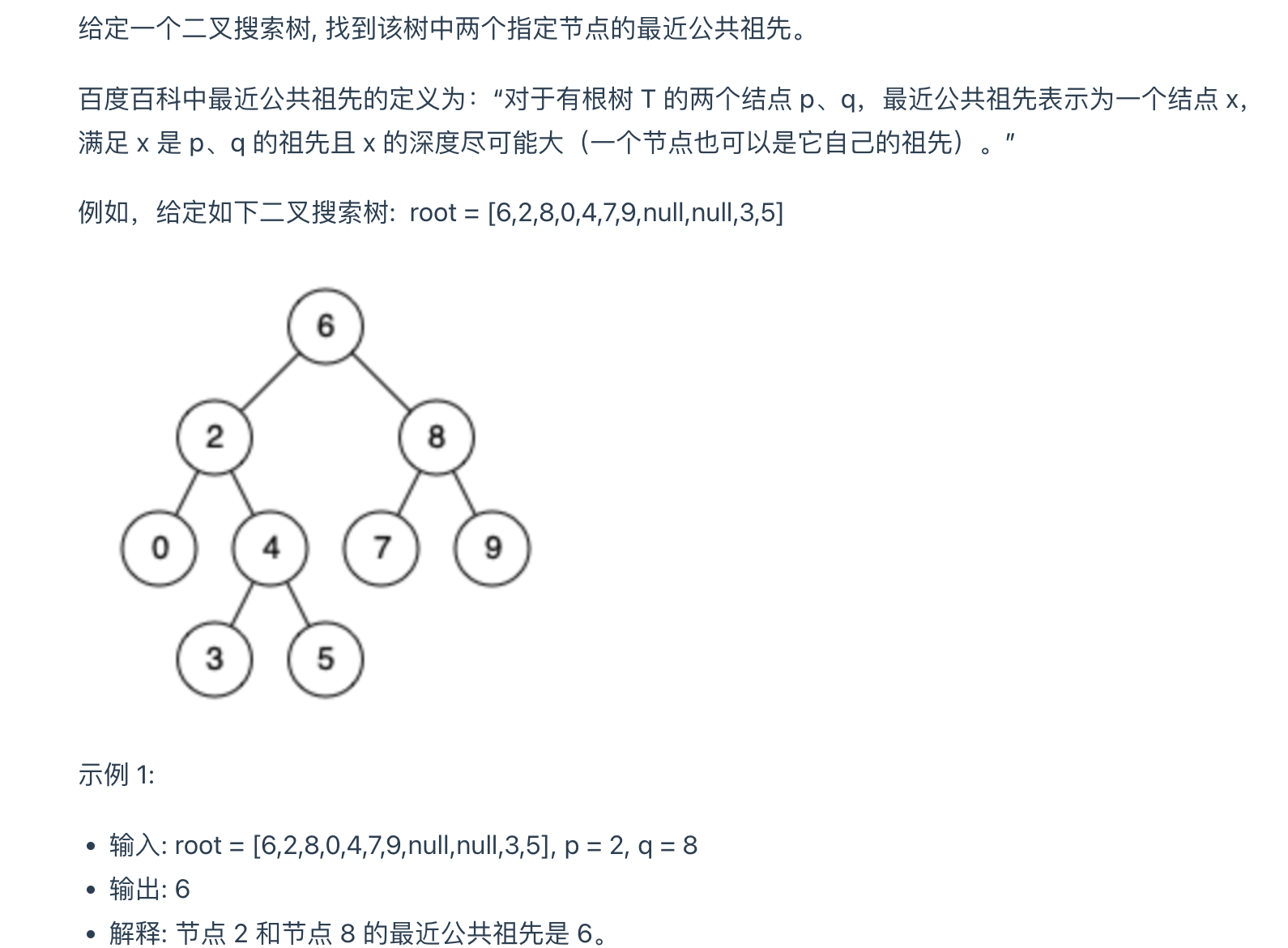思路：二叉搜索树自带方向性，可以方便的从上向下查找目标区间，遇到目标区间内的节点，直接返回。

class Solution:
    def lowestCommonAncestor(self, root, p, q):
        if root.val > p.val and root.val > q.val:
            return self.lowestCommonAncestor(root.left, p, q)
        elif root.val < p.val and root.val < q.val:
            return self.lowestCommonAncestor(root.right, p, q)
        else:
            return root

701. 二叉搜索树中的插入操作

递归：

class Solution:
    def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
        if root is None or root.val == val:
            return TreeNode(val)
        elif root.val > val:
            if root.left is None:
                root.left = TreeNode(val)
            else:
                self.insertIntoBST(root.left, val)
        elif root.val < val:
            if root.right is None:
                root.right = TreeNode(val)
            else:
                self.insertIntoBST(root.right, val)
        return root

迭代：

class Solution:
    def insertIntoBST(self, root, val):
        if root is None:  # 如果根节点为空，创建新节点作为根节点并返回
            node = TreeNode(val)
            return node

        cur = root
        parent = root  # 记录上一个节点，用于连接新节点
        while cur is not None:
            parent = cur
            if cur.val > val:
                cur = cur.left
            else:
                cur = cur.right

        node = TreeNode(val)
        if val < parent.val:
            parent.left = node  # 将新节点连接到父节点的左子树
        else:
            parent.right = node  # 将新节点连接到父节点的右子树

        return root

450. 删除二叉搜索树中的节点

递归三部曲：

• 确定递归函数参数以及返回值

说到递归函数的返回值，也可以通过递归返回值删除节点。

• 确定终止条件

遇到空返回，其实这也说明没找到删除的节点，遍历到空节点直接返回了

• 确定单层递归的逻辑

这里就把二叉搜索树中删除节点遇到的情况都搞清楚。

有以下五种情况：

• 第一种情况：没找到删除的节点，遍历到空节点直接返回了

• 找到删除的节点

  • 第二种情况：左右孩子都为空（叶子节点），直接删除节点， 返回NULL为根节点

  • 第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点

  • 第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点

  • 第五种情况：左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。

读完本篇，大家会发现二叉搜索树删除节点比增加节点复杂的多。

因为二叉搜索树添加节点只需要在叶子上添加就可以的，不涉及到结构的调整，而删除节点操作涉及到结构的调整。

这里我们依然使用递归函数的返回值来完成把节点从二叉树中移除的操作。

这里最关键的逻辑就是第五种情况（删除一个左右孩子都不为空的节点），这种情况一定要想清楚。

递归法：

class Solution:
    def deleteNode(self, root, key):
        if root is None:
            return root
        if root.val == key:
            if root.left is None and root.right is None:
                return None
            elif root.left is None:
                return root.right
            elif root.right is None:
                return root.left
            else:
                cur = root.right
                while cur.left is not None:
                    cur = cur.left
                cur.left = root.left
                return root.right
        if root.val > key:
            root.left = self.deleteNode(root.left, key)
        if root.val < key:
            root.right = self.deleteNode(root.right, key)
        return root

迭代法：

class Solution:
    def deleteOneNode(self, target: TreeNode) -> TreeNode:
        """
        将目标节点（删除节点）的左子树放到目标节点的右子树的最左面节点的左孩子位置上
        并返回目标节点右孩子为新的根节点
        是动画里模拟的过程
        """
        if target is None:
            return target
        if target.right is None:
            return target.left
        cur = target.right
        while cur.left:
            cur = cur.left
        cur.left = target.left
        return target.right

    def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
        if root is None:
            return root
        cur = root
        pre = None  # 记录cur的父节点，用来删除cur
        while cur:
            if cur.val == key:
                break
            pre = cur
            if cur.val > key:
                cur = cur.left
            else:
                cur = cur.right
        if pre is None:  # 如果搜索树只有头结点
            return self.deleteOneNode(cur)
        # pre 要知道是删左孩子还是右孩子
        if pre.left and pre.left.val == key:
            pre.left = self.deleteOneNode(cur)
        if pre.right and pre.right.val == key:
            pre.right = self.deleteOneNode(cur)
        return root